Modern cryptography is threatened by the arrival of quantum computers. Indeed, Shor’s quantum algorithm (a quantum algorithm) can be used to break modern cryptography in polynomial time due to a quantum boost in the factorization problem. As a response, the National Institute of Standards and Technology (NIST) launched a call for standardization of quantum-resistant algorithms. In 2020, the candidates of the third round were announced, and Supersingular Isogeny Key Encapsulation (SIKE) is one of the schemes that were announced as alternative candidates (i.e., those which were not rejected but not finalists as well).
In this series of blog posts, we will explain a power analysis attack on SIKE based on the paper Full key recovery side-channel attack on ephemeral SIKE by A. Genêt, N. Kaluđerović, and N. Linard.
In this post, we start by giving an introduction on isogeny-based cryptography.
In the case of our blog post, an isogeny φ: E -> E can be thought of as a map between two elliptic curves. Isogeny-based cryptography relies on the quantum-resistant hard problem of finding the unique isogeny between two arbitrary curves. As a result, one can design a cryptosystem in which two participants exchange curves related to secret isogenies and reach a shared secret in a Diffie–Hellman fashion.
Isogeny-based cryptography is a young field. The first cryptosystem was developed by Couveignes in 1997 and then rediscovered in 2006 by Rostovsev and Stolbunov. While the original schemes used ordinary elliptic curves, Jao and De Feo used a special kind of curves (supersingular elliptic curves) to prevent a subexpoential-time quantum attack discovered in 2014 by Childs, Jao, and Soukharev. The resulting scheme is called SIDH (Supersingular Isogeny Diffie-Hellman) and works as a key exchange mechanism based on Diffie–Hellman.


SIDH is a public-key protocol that involves two parties (by convention, Alice and Bob) who both possess a personal key-pair (private and public keys) and which can therefore be set up in three different settings:
Because plain SIDH is insecure both in static and in semi-static settings, SIDH needs to be used in a certain way to obtain a secure key exchange; namely with the Fujisaki–Okamoto transform. This transform works by re-encrypting ciphertexts to make sure that a malicious party is not trying to deceive the other with counterfeit ciphertexts. Applied to SIDH, the Fujisaki–Okamoto transform gives rise to SIKE (Supersingular Isogeny Key Exchange), the very cryptosystem that was submitted to the NIST standardization process and the one that we consider in this blog post.
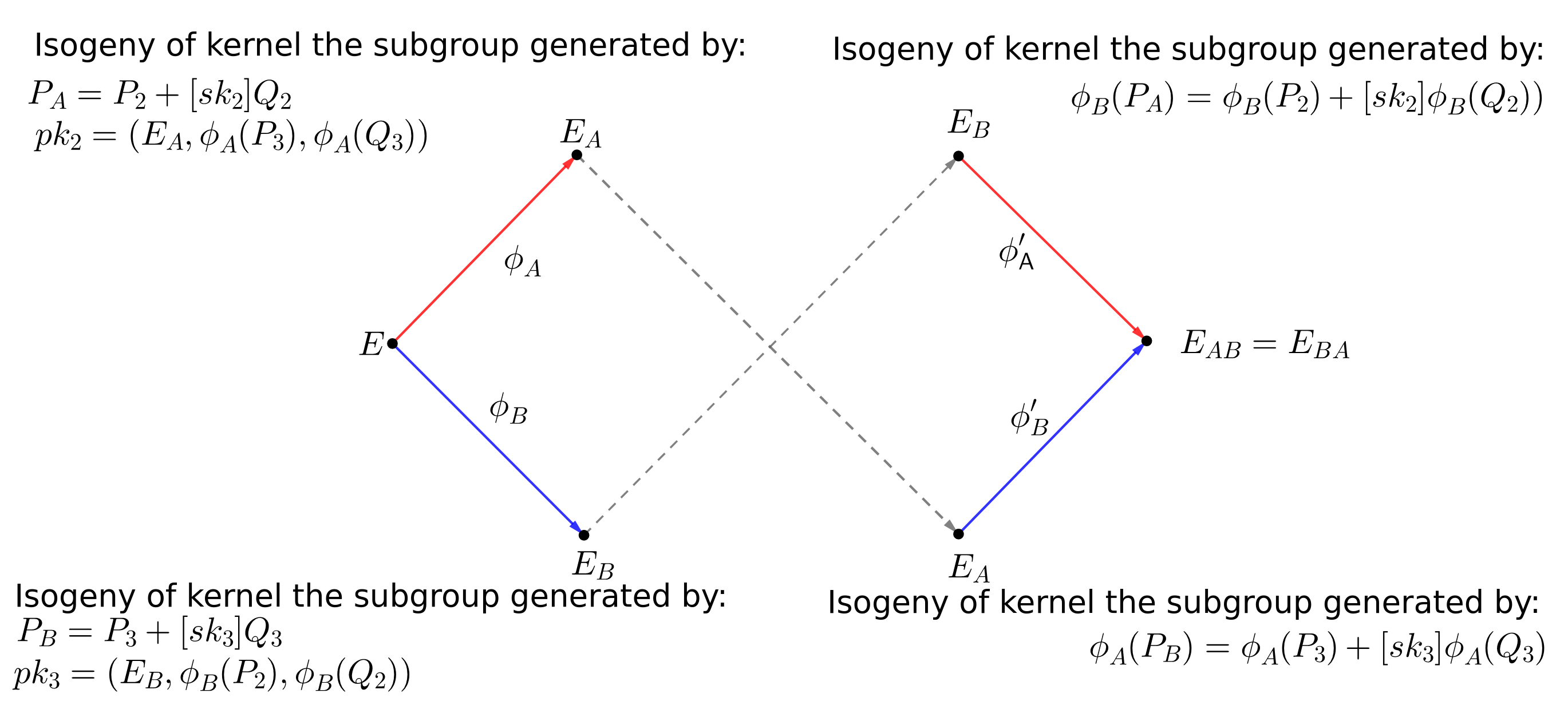
The public parameters of SIKE encompass a prime number p = 2n3m ± 1, a starting elliptic curve E0, basis elliptic curve points (PA, QA) of the torsion subgroup E[2n], and basis elliptic curve points (PB, QB) of the torsion subgroup E[3m].
Recall from classical elliptic curve cryptography, an elliptic curve (E, +, O) is a set of points of the form P = (x, y) which satisfy an elliptic curve equation (such as x² = x³ + ax + b) along with a special point O known as the point to infinity. The particularity of elliptic curves is that two points P, Q ∈ E can be added together to create a third point which will also belong to the elliptic curve. More particularly, adding the same point to itself an arbitrary number of times (such as k times) leads to another point also on the elliptic curve (P + P + … + P = [k]P ∈ E). The point to infinity O acts as the zero element on the curve (i.e., P + O = O + P = P for any point P ∈ E).
In SIDH, Bob starts by generating a random integer sk3, and finds the secret point PB on E0 by computing P3 + [sk3]Q3. This resulting point allows Bob to compute his secret isogeny φB, and so Bob can send the resulting elliptic curve φB(E0) = EB to Alice. Alice, in parallel, can perform identical operations with her own secret key and secret isogeny, and sends her resulting elliptic curve φA(E0) = EA to Bob. Both can compound their own isogeny from their received elliptic curves to obtain a final common curve, i.e., φB(EA) = φA(EB) = EAB. Since neither φA nor φB can be recovered from the communication, the final curve EAB is secret and can be used to derive a shared secret key.
In the next blog, we will talk about side-channel attacks and how such attacks can be applied to SIKE to obtain a secret key processed by a party.
CYSEC LAB is a security evaluation lab performing research of front-edge technologies. The team, made of embedded engineers, security researchers and cryptographers, has the complementary skills that allows CYSEC to engineer and develop home made test benches with high performance.
For more information, please visit: www.cysec.com/lab/
Media Contact
Alexandre Karlov